二进制整数转化十进制
在数字世界中,二进制和十进制是两种最为常见的数制。其中,将二进制整数转化为十进制是一项基础而重要的技能,它不仅在计算机科学中有着广泛的应用,对于我们理解数字的本质和运算规律也具有重要意义。
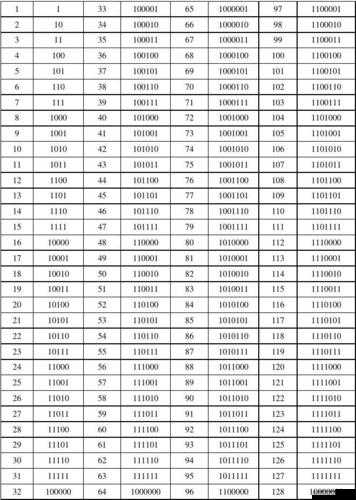
二进制,作为计算机内部处理信息的基本数制,由 0 和 1 两个数字组成。而十进制则是我们日常生活中最常用的数制,由 0 到 9 十个数字构成。理解二进制整数转化为十进制的过程,就像是打开了一扇通往数字世界深层奥秘的大门。
让我们从最基础的原理开始。二进制整数转化为十进制的核心在于位权的概念。在二进制中,从右往左,每一位的位权依次是 2 的 0 次方、2 的 1 次方、2 的 2 次方,以此类推。例如,二进制数 1010 ,最右边的 0 位权是 2 的 0 次方即 1 ,右边第二位的 1 位权是 2 的 1 次方即 2 ,第三位的 0 位权是 2 的 2 次方即 4 ,最左边的 1 位权是 2 的 3 次方即 8 。
那么如何具体进行转化呢?我们以二进制数 1101 为例。将每一位数字乘以其对应的位权,然后将所得的结果相加。最右边的 1 乘以 2 的 0 次方得到 1 ;右边第二位的 0 乘以 2 的 1 次方得到 0 ;第三位的 1 乘以 2 的 2 次方得到 4 ;最左边的 1 乘以 2 的 3 次方得到 8 。最后将这四个结果相加:1 + 0 + 4 + 8 = 13 ,所以二进制数 1101 转化为十进制就是 13 。
掌握了这个基本方法,我们可以处理更复杂的二进制整数。比如,二进制数 101011 ,按照上述方法,最右边的 1 乘以 1 得到 1 ;右边第二位的 1 乘以 2 得到 2 ;第三位的 0 乘以 4 得到 0 ;第四位的 1 乘以 8 得到 8 ;第五位的 0 乘以 16 得到 0 ;最左边的 1 乘以 32 得到 32 。相加可得:1 + 2 + 0 + 8 + 0 + 32 = 43 ,即二进制数 101011 转化为十进制是 43 。
在实际应用中,二进制整数转化为十进制的能力具有重要的意义。在计算机编程中,我们经常需要处理二进制数据,并将其转化为十进制以便于理解和处理。例如,当我们读取一个二进制文件中的数据时,可能需要将其中的二进制整数转化为十进制来进行后续的计算和分析。
在密码学中,二进制的运算和转化也扮演着关键的角色。加密和解密的过程中,常常涉及到对二进制数据的操作和转换。
对于学习数学和计算机科学的学生来说,熟练掌握二进制整数转化为十进制不仅有助于理解相关的理论知识,还能提高解决实际问题的能力。通过不断地练习和实践,可以提高转化的速度和准确性,为更深入的学习和研究打下坚实的基础。
有趣的是,二进制的世界里还隐藏着许多奇妙的规律和现象。比如,通过二进制的转化,我们可以发现数字之间的特殊关系,这对于探索数学的奥秘有着独特的魅力。
二进制整数转化为十进制虽然看似简单,但却是数字世界的基石之一。无论是在学术研究、技术应用还是日常生活的某些领域,它都发挥着不可或缺的作用。希望能够让您对这一重要的数字转化过程有更深入的理解和认识,并且能够在实际中灵活运用,开启您探索数字世界的精彩之旅。







